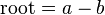El
cálculo mental consiste en realizar
cálculos matemáticos utilizando sólo el
cerebro, sin ayudas de otros instrumentos como
calculadoras
o incluso lápiz y papel. Algunos calculistas pueden realizar
operaciones matemáticas muy complejas (como productos de números de 4 o
más cifras) mediante el cálculo mental. Sin embargo, los mejores
matemáticos muchas veces no coinciden con
los mejores calculistas. La práctica del cálculo mental favorece que el estudiante ponga en juego diversas
estrategias. Es la actividad matemática más
cotidiana y la menos utilizada en el áula. Entre sus beneficios se encuentran: desarrollo del
Sentido Numérico y de habilidades intelectuales como la
atención y la
concentración,
además de gusto por las Matemáticas. Para su enseñanza es aconsejable
permitir el descubrimiento de reglas y la selección de estrategias. Aquí
se presentan algunas formas de entrenar el cálculo mental.
Sumas y restas
Si no hay
acarreos, es decir, si ninguna suma parcial es mayor que 9, las sumas se pueden realizar directamente. Lo mismo ocurre con las restas.
En caso contrario, hay que saber modelar los números de los que se
dispone, a veces convirtiendo una suma de dos números en una suma más
sencilla de más sumandos, y algo análogo para las restas. Calculistas
como
Alberto Coto proponen realizar las sumas siempre de izquierda a derecha, aunque haya acarreos.
Ejemplos:
- 456 + 155 = 461 + 150 = 511 + 100 = 611 (método tradicional, sumando de derecha a izquierda)
- 456 + 155 = 456 + 4 + 151 = 460 + 40 + 111 = 500 + 111 = 611
(llevando el primer sumando a la decena superior, a la centena
superior... para acabar realizando una suma más sencilla equivalente a
la primera)
- 456 + 155 = 556 + 55 = 606 + 5 = 611 (sumando de izquierda a derecha)
- 876 - 98 = 868 - 90 = 778 (método tradicional, de derecha a izquierda)
- 876 - 98 = 876 - (100 - 2) = 876 - 100 + 2 = 776 + 2 = 778
(valiéndose de la proximidad del sustraendo (98) a uno que facilita la
resta (100))
- 876 - 98 = 786 - 8 = 778 (restando de izquierda a derecha)
- 634 - 256 = 434 - 56 = 384 - 6 = 378 (de izquierda a derecha)
Duplicación y mediación
Multiplicar por 2 es lo mismo que sumarle al número inicial el mismo
número. La duplicación y la mediación son un pilar fundamental de las
matemáticas egipcias.
Ejemplo: multiplicar 173 × 16:
- Esto se puede hacer por duplicaciones sucesivas: 173 × 16 = 346 × 8 = 692 × 4 = 1384 × 2 = 2768.
La multiplicación y la mediación sirven, en general, para calcular el producto de un número cualquiera por el producto de
potencias
de 2 y de 5. Multiplicar por 5 es lo mismo que calcular la mitad del
número inicial multiplicado por 10, lo que a veces es más fácil de
hallar.
Ejemplo: multiplicar 376 × 125
- Como 125 = 5³ = 10³/2³, se puede hallar la solución añadiendo los
tres ceros correspondientes y dividiendo el resultado tres veces por 2.
- 376 × 125 = 376000/8 = 188000/4 = 94000/2 = 47000.
- 324 x 125 = 324000/8 = 162000/4 = 81000/2 = 40500.
Es útil conocer algunas potencias de 2 y 5 para realizar estas operaciones con soltura.
También se puede utilizar este método para multiplicar por otros
números que son sumas de (pocas) potencias de 2 o de 5, como 12 (8 + 4),
130 (125 + 5), 18 (16 + 2), etc.
Multiplicación por números cercanos a las potencias de 10
Multiplicar por 9, 11, 99, 101..., es decir, por una potencia de 10
menos 1, se puede hacer mentalmente con un poco de práctica mediante la
suma (o resta) de 10
n veces el número inicial más (o resta)
del número inicial. Sin embargo, es fácil cometer errores al sumar o
restar al mezclar, por ejemplo, unidades con decenas.
Ejemplo: multiplicar 28 × 99
- 28 × 99 = 28 × (100 - 1) = 2800 - 28 = 2772
Otro ejemplo: multiplicar 37 × 121
- 121 es el cuadrado de 11, así que lo que se pide es lo mismo que
multiplicar 37 por 11 y el resultado de nuevo por 11: 37 × 121 = 37 ×(10
+ 1) × 11 = (370 + 37) × 11 = 407 × 11 = 4477
Además multiplicar por 11 resulta fácil: se separan las cifras y
luego se escribe siempre cifra de las unidades y seguidamente se van
sumando grupos de dos cifras seguidas poniendo el resultado o la última
cifra de la suma llevando un acarreo de 1 si la suma es mayor que 10, y
finalmente se coloca la cifra más significativa, así:
Multiplicar:
- 12345 × 11 : 1° las unid 5, 5+4=9, 4+3=7, 3+2=5,2+1=3, y finalmente 1; ahora colocar en orden inverso : 135795
- 8946 × 11 : 1° las unid 6, 6+4=10 (0 y lleva 1), 4+9+1(acarreo)=14
(4 y lleva 1), 9+8+1(acarreo)=18 (8 y lleva 1), y finalmente
8+1(acarreo)=9; ahora colocar en orden inverso : 98406
Análogamente, se puede aplicar esto a las multiplicaciones por potencias de 2, o de 5, más 1. Por ejemplo, 26, 17, 124 y 63.
Multiplicación por 37
Primero, basta recordar lo siguiente:
- 37 × 3 = 111
- 37 × 27 = (37 × 3) × 9 = 999 = 1000 - 1
El procedimiento es este:
- Se divide el otro factor entre 3. Hay que recordar el cociente y el
resto. Si el resto es 1, al resultado final habrá que sumar 37; si es 2,
habrá que sumar 74.
- Ejemplo: en 37 × 94, se toma 94 : 3 = 31, resto 1. Ahora el producto es 111 × 31.
- Se divide el cociente del paso anterior entre 9. El cociente se multiplica por 999 (= 1000 - 1) y el resto por 111.
- En el ejemplo anterior, 31 : 9 = 3, resto 4. Ahora tenemos la suma
de dos productos: 999 × 3 (= 2997, o, si se prefiere, 3000 - 3) y 111 × 4
= 444. Como el resto del primer cociente que hicimos era 1, al
resultado habrá que sumar 37.
- Se suma todo.
- 3000 - 3 + 444 + 37 = 3000 + 444 + 37 - 3 (a menudo es más fácil
organizar los términos de esta forma, dejando el número que se resta al
final) = 3444 + 34 = 3478.
Una variante es tomar por exceso y no por defecto el cociente de la
división del primer paso. Esto significa que se suma uno al cociente y
al resto se le restan 3. Así, en lugar de un número de la forma 3 ×
Q + R (donde R = 1 ó 2) tenemos uno de la forma 3 × (
Q + 1) + R' (donde R' = -2 ó -1, respectivamente), y al resultado final se le
restará 74 o 37 (porque el nuevo "resto" de la división es negativo).
Más ejemplos:
- 37 × 54 = 111 × 18 = 999 × 2 = 2000 - 2 = 1998
- 37 × 79 (método usual) = 111 × 26 + 37 = 999 × 2 + 111 × 8 + 37 = 2000 - 2 + 888 + 37 = 2925 - 2 = 2923
- 37 × 79 (variante) = 111 × 27 - 74 = 999 × 3 - 74 = 3000 - 3 - 74 = 3000 - 77 = 2923
- Como se puede comprobar, en este caso la variante es más fácil,
aunque no tiene por qué ser siempre así. En general, si el factor es uno
o dos menos que un múltiplo de 27 (recordar que 37 × 27Q = 999Q), es más sencillo ir a por ese múltiplo de 27.
Si uno de los factores del producto no es 37 pero sí un múltiplo, se
puede reformular la multiplicación haciendo que uno de los factores sea
37. Probemos por ejemplo con los siguientes cuadrados:
- 74 × 74 = 37 × 2 × 74 = 37 × 148 = 111 × 49 + 37 = 999 × 5 + 111 × 4 + 37 = 5000 - 5 + 444 + 37 = 5444 + 32 = 5476
- 111 × 111 = 37 × 3 × 111 = 37 × 333 = 999 × 12 + 333 = 12000 - 12 + 333 = 12321 (en este caso, como ya teníamos el 333, el procedimiento era más sencillo)
- 148 × 148 = 37 × 4 × 148 = 37 × 592 = 111 × 198 - 74 (en este
caso se vuelve a emplear la variante porque 594 es múltiplo de 27) =
999 × 22 - 74 = 22000 - 22 - 74 = 21904
Métodos así funcionan cuando uno de los factores de la multiplicación
tiene a su vez un múltiplo que es una concatenación de nueves. Se trata
pues de encontrar ese múltiplo. Otro ejemplo notable es el número
142857.
No sólo el producto de este número por 7 es igual a 999999, sino que su
tabla de multiplicar es muy sencilla, ya que en la cadena
142857142857... basta con tomar seis dígitos consecutivos a partir de
una posición dada:
- 142857 × 1 = 142857
- 142857 × 2 = 285714
- 142857 × 3 = 428571
- 142857 × 4 = 571428
- 142857 × 5 = 714285
- 142857 × 6 = 857142
Probemos a calcular el cuadrado de este número de seis cifras (!):
- 142857 × 142857 = (142857 × 7) × (142857 : 7) = 999999 × 20408 +
142857 (Como el resto de 142857 : 7 da 1, al resultado de la
multiplicación hay que sumarle 142857. Es lo mismo que se hacía en la
multiplicación por 37) = (1.000.000 - 1) × 20.408 + 128.857 =
20.408.000.000 - 20.408 + 142857 = 20.408.000.000 + 122.449 =
20.408.122.449
Igualdades notables y cálculo de cuadrados
Las llamadas
igualdades notables pueden aplicarse al cálculo mental:
- (a + b)² = a² + 2ab + b²
- (a - b)² = a² - 2ab + b²
- (a + b) (a - b) = a² - b²
Cálculo del cuadrado de un número cualquiera de dos cifras
Las dos primeras identidades se pueden aplicar al cálculo de
cuadrados perfectos. Supongamos que queremos calcular 52². 52 = 50 + 2,
así que aplicamos la identidad correspondiente al cuadrado de la suma,
donde
a = 50 y
b = 2.
- (50 + 2)² = 50² + 2 × 2 × 50 + 2² = 2500 + 200 + 4 = 2704
Más ejemplos:
- 17² = (10 + 7)² = 10² + 2 × 7 × 10 + 7² = 100 + 140 + 49 = 289
- 76² = (70 + 6)² = 70² + 2 × 6 × 70 + 6² = 4900 + 840 + 36 = 5776
- 95² = (90 + 5)² = 90² + 2 × 5 × 90 + 5² = 8100 + 900 + 25 = 9025
Con este método también es fácil calcular el cuadrado de un número
con una cifra entera y una decimal, sólo hay que acordarse del lugar que
ocupa cada cifra:
- 2,4² = (2 + 0,4)² = 0,1² × 14² = 0,01 × (20² + 2 × 4 × 20 + 4²) = 0,01 × (400 + 160 + 16) = 0,01 × 576 = 5,76
Algoritmo para elevar al cuadrado un número de dos cifras que empieza
con 4: (4*10+u)^2 = (15+u) y (10-u)^2 Ejemplo: 47^2= (15+7) y (10-7)^2 =
22 y 09 =2209, ya que 47^2= 40x40 + 40x7x2 + 7x7 = 1600 + 560 + 49 =
2209.
Algoritmo idem, para los que empieza con 5.- (5*10+u)^2 =(25+u) y u^2; ejemplo: 53^2= (25+3) y 3^2 = 2809
Algoritmo idem, para los que empiezan con 9.- (9*10+u)^2= (80+2u)y(10-u)^2; ejemplo: 96^2=(80+2*6)y(10-6)^2= 92y16= 9216
Algoritmo idem,para los de tres cifras que empieza con 10.-
(10*10+u)^2= (100+2u)y u^2; ejemplo 108^2= (100+2*8)y8^2 = 116y64= 11664
Algunos calculistas conocen de memoria las
tablas de multiplicar
del 1 al 100, por lo que pueden utilizar este método fácilmente para
hallar el cuadrado de un número de cuatro cifras o más. Esto sólo se
consigue tras mucho entrenamiento, pero simplifica enormemente el
cálculo como se puede observar:
- 5782² = (5700 + 82)² = 5700² + 2 × 82 × 5700 + 82² = 32.490.000 + 934.800 + 6.724 = 33.431.524
Producto de dos números que equidistan de un número cuyo cuadrado es conocido
El número cuyo cuadrado es conocido generalmente será uno acabado en
0. Por ejemplo, a la hora de calcular 58 × 62 nos apoyaremos en el 60,
ya que ambos están a la misma distancia (2 unidades) de 60. Aquí se
puede utilizar la tercera identidad, la del producto de suma por
diferencia, donde
a = 60 y
b = 2.
- (60 + 2) (60 - 2) = 60² - 2² = 3600 - 4 = 3596
Más ejemplos:
- 77 × 83 = (80 - 3) (80 + 3) = 6400-9= 6391
- 95 × 105 = (100 - 5) (100 + 5) = 10000-25= 9975
- 128 × 152 = (140 - 12) (140 + 12) = 19600-144= 19456
Cuadrado de un número acabado en 5
El cálculo del cuadrado de un número que acabe en 5 puede simplificarse utilizando la tercera identidad. Aquí
a será el número inicial (por ejemplo, 65), y
b = 5:
- (a + 5) (a - 5) = a² - 25
Por tanto, se tiene que:
- (a + 5) (a - 5) + 25 = a²
Si
a = 65, el resultado es el siguiente:
- 65² = 70 × 60 + 25 = 4200 + 25 = 4225.
Más ejemplos:
- 35 × 35 = 40 × 30 + 25 = 1225
- 105 × 105 = 110 × 100 + 25 = 11025
- 255 × 255 = 260 × 250 + 25 = 65025
- En este último caso, para calcular 260 × 250 se puede optar por
formularlo de esta manera: 260 × 250 = (250 + 10) × 250 = 250² + 2500, y
ya sabemos calcular con facilidad 250², así, quedaría 62500 + 2500 + 25
= 65025.
Cubos y potencias superiores
El cálculo de cubos y potencias superiores mediante el uso de
igualdades notables
es progresivamente más difícil, y a menudo es más sencillo hallar la
cuarta potencia de un número como el cuadrado de su cuadrado:
- 954 = (95²)² = 9025² = (9000 + 25)² = 9000² + 2 × 25 ×
9000 + 25² = 81.000.000 + 450.000 + 625 = 81.450.625 (Facilita mucho el
cálculo el hecho de que la segunda cifra de 9025 sea un cero)
Cálculo de logaritmos (en base 10)
Para aproximar el
logaritmo común o en
base 10 con una o dos
cifras significativas,
se requiere conocer algunas propiedades de los logaritmos y la
memorización de algunos logaritmos. En particular, es necesario saber lo
siguiente:
- log(ab) = log(a) + log(b)
- log(a : b) = log(a) - log(b)
- log(0) si existe
- log(1) = 0
- log(2) ~ 0,33
- log(3) ~ 0,48
- log(7) ~ 0,85
- log(10) = 1
- Si a > b, forzosamente log(a) > log (b). En lenguaje matemático, se dice que la función logaritmo es creciente.
A partir de esta información, se puede calcular el logaritmo de cualquier número del 1 al 9:
- log(1) = 0
- log(2) ~ 0,30
- log(3) ~ 0,48
- log(4) = log(2 × 2) = log(2) + log(2) ~ 0,60
- log(5) = log(10 : 2) = log(10) - log(2) ~ 0,70
- log(6) = log(2 × 3) = log(2) + log(3) ~ 0,78
- log(7) ~ 0,85
- log(8) = log(2 × 2 × 2) = log(2) + log(2) + log(2) ~ 0,90
- log(9) = log(3 × 3) = log(3) + log(3) ~ 0,96 (en realidad, se acerca más a 0,95)
- log(10) = 1
El primer paso para aproximar el logaritmo común de un número es expresar dicho número en la
notación científica. Por ejemplo, el número 45 en notación científica es 4,5 × 10
1. En general, tendremos un número de la forma
a × 10
b, donde
a es un número entre 1 y 10. El segundo paso es utilizar lo que se llama
interpolación lineal
para estimar el logaritmo que queramos calcular a partir de dos ya
conocidos. En el ejemplo del 45 (= 4,5 × 10), se parte de que log(4) ~
0,60 y log(5) ~ 0,70, y como 4,5 está a medio camino entre 4 y 5,
log(4,5) estará aproximadamente a medio camino entre log(4) y log(5),
por tanto, será aproximadamente 0,65. En realidad, el resultado correcto
siempre es ligeramente mayor de lo esperado, de hecho, log(4,5) =
0,6532125... El tercer y último paso, una vez obtenido log(
a), es sumarle
b
para obtener el logaritmo deseado. En este caso, como log(4,5) ~ 0,65,
basta añadir 1 para obtener log(45) ~ 1,65. El valor real es log(45) ~
1,6532125...
El mismo proceso se puede emplear para calcular el logaritmo de un
número entre 0 y 1. Por ejemplo, 0,045 en notación científica se expresa
como 4,5 × 10
-2. Hay que tener cuidado con este exponente, que es negativo. Esto dará lugar al resultado log(0,045) ~ 0,65 - 2 = -1,35.
Otro método es calcular el logaritmo del número a partir de una
factorización de números cuyos logaritmos sean conocidos. En el ejemplo
anterior, 45 = 9 × 5, por tanto, log(45) = log(9) + log(5) ~ 0,96 + 0,70
= 1,66.
Verificar el resultado
Hay varias formas de comprobar si el resultado al que se ha llegado es el correcto:
- Orden de magnitud:
Si, tras multiplicar dos números menores de 100, el resultado es mayor
de 10.000, seguro que hay algún problema. En una multiplicación de dos
factores, hay que comprobar que el resultado tiene un número de cifras
igual, o una unidad mayor (según el caso) que la suma de las cifras de
los factores. A menudo los errores en el orden de magnitud se deben a
una mala posición de uno de los números a la hora de sumar los productos
parciales. Por ejemplo, multiplicar 65 × 205 en lugar de 65 × 25, o
viceversa.
- Cifra de las unidades: Consiste en comprobar que la última cifra del
resultado es correcta vista la última cifra de cada uno de los números
con que se parte. Por ejemplo, 73 × 64 debe terminar en 2, ya que 3 × 4 =
12. Esta verificación permite conocer una cifra con certeza.
- Prueba del nueve:
Esta verificación se basa en la suma de las cifras de cada uno de los
factores y del resultado hasta que sólo queden números de una cifra. Por
ejemplo, si nos queda 73 × 64 = 4662, podemos comprobar si es cierto
sumando las cifras de cada uno de los números:
-
- 7 + 3 = 10, 1 + 0 = 1
- 6 + 4 = 10, 1 + 0 = 1
- 4 + 6 + 6 + 2 = 18, 1 + 8 = 9
- Sin embargo, 1 × 1 no es igual a 9, así que el resultado no es
correcto. Habría que revisar de nuevo la multiplicación o realizarla de
nuevo. (El resultado correcto es 4672) Este método es bueno para
detectar errores de acarreo.
Conclusión
En general, el cálculo mental consiste en modelar los números de la
forma más conveniente para realizar las operaciones prescritas. Para
desarrollar una mayor agilidad en el cálculo mental, es útil:
- Conocer algunas potencias de números pequeños, como 2, 3 y 5. En
muchos casos, un producto se puede escribir de otra forma más
conveniente si se juega con los factores. Por ejemplo, 65 × 27 es más
fácil de calcular si se entiende el producto por 27 como productos
sucesivos por 3.
- Conocer algunos cuadrados y saber utilizar las igualdades notables y la propiedad distributiva
de la multiplicación para simplificar el cálculo. Por ejemplo, 13 × 18
es lo mismo que 13 × (17 + 1) = 13 × 17 + 13. Mediante las igualdades
notables, 13 × 17 = 225 - 4 = 221, así que el resultado final es 234.


















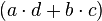


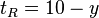


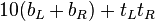
![\, = 10 [(x-5) + (y-5)] + (10-X) (10-y)](http://upload.wikimedia.org/wikipedia/en/math/b/5/0/b506130b3f17c087d32cff3bf4889e12.png)

![\, = [10 (x + y) - 100] + [100 - 10 (x + y) + xy]](http://upload.wikimedia.org/wikipedia/en/math/5/d/e/5de767bc2b44cf2ea9b03dc6829ffc49.png)
![\, = [10 (x + y) -10 (x + y)] + [100-100] + xy](http://upload.wikimedia.org/wikipedia/en/math/6/0/1/60186e041fe6b8980c94964fd4c05754.png)