Antes de empezar con los mnemónicos hablaré un poco sobre lo
que es la abstracción, veamos una definición; (del lat. abstractio = sacar fuera de) es un proceso que
implica reducir los componentes fundamentales de información de un fenómeno
para conservar sus rasgos más relevantes con el objetivo de formar categorías o
conceptos. Por ejemplo si tomamos la siguiente secuencia o serie: palmera,
sauce, roble, manzano... podemos tomar ciertas características como la raíz, el
tronco, las ramas, hojas, fruto etc. y según esto abstraer un “árbol ideal” que
nos serviría de molde para poder identificar a otras especies, clasificar o
incluso descubrir nuevas. Así se puede abstraer características o patrones de
los operadores matemáticos, observamos a los signos +, - , X, / etc. y definimos un
operador abstracto * que
podría representar desde el conocido signo “+” (operador suma) hasta, por
ejemplo, un giro en el cubo rubik. Otro ejemplo más para que quede bien claro,
tomemos los cuerpos de números naturales |N, reales |R y complejos |C. Una característica de todos ellos es que
existen la suma y multiplicación, pero por ejemplo dos números naturales
divididos no dan otro natural, ejemplo 1/2 = 0.5 no pertenece a los naturales sino a los
racionales. Así podemos definir un cuerpo de números G abstracto con el cual
trabajaremos propiedades de estos cuerpos de una manera más general.
Empecemos con estos axiomas donde G es un cuerpo más general
que no son ni los reales ni complejos etc. y el operador O que tampoco es
ninguno de los conocidos sino algo más abstracto:
Grupos
Un grupo 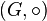 es un conjunto G en el que se ha definido una ley de composición interna
es un conjunto G en el que se ha definido una ley de composición interna  que satisface los siguientes axiomas:
que satisface los siguientes axiomas:
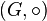 es un conjunto G en el que se ha definido una ley de composición interna
es un conjunto G en el que se ha definido una ley de composición interna  que satisface los siguientes axiomas:
que satisface los siguientes axiomas:
Por lo tanto, un grupo está formado por un conjunto de elementos abstractos o símbolos, y por una ley de composición interna (operación binaria) que los relaciona. Dicha ley de composición interna indica cómo deben ser manipulados los elementos del grupo.
Se dice que un grupo es abeliano o conmutativo cuando verifica además la propiedad conmutativa:
Para comenzar asociaré 1
con la propiedad asociativa, en
el código que manejo 1 = t, es decir té (la
vocal no cuenta) así imagino a un grupo de ingleses asociándose a las 5 pm. Para tomar el té.
2 = n, es decir
“ano” me imagino expeliendo elementos neutrones por el ano. Estas asociaciones cuasi-escatológicas que nos mueven a la risa
son las más efectivas.
3 = mear, aquí
uso una consonante la “r” que es el número cero pero esta vez podemos obviar,
no podemos ser tan estrictos siguiendo
las reglas, siempre y cuando no nos confundamos. Aquí podría imaginarme “meando
a un simio rico (simet-rico)” entonces esto me ayudaría a recordar que la
propiedad 3 es la del elemento simétrico.
4 = Oca, Aquí
podemos imaginar a Abel (para hacernos una idea del matemático Niels Hendrik
Abel, podemos buscar en imágenes google para reforzar nuestra asociación;
información adicional como la extrema pobreza en la que vivió nos puede servir
para hacernos de un contexto) Así imaginamos a Abel con su oca
poniéndola sobre un conmutador (una
especie de motor-interruptor) para hacerlo funcionar. Y ya tenemos la asociación
4 -oca-Abel-conmutativo.
Para axiomas de números reales ya no son 4 sino 8 (es decir,
4 para el operador suma y 4 para el operador multiplicación) sin embargo, aquí hay
algunas variaciones según los autores, pues muchos empiezan con el axioma de
clausura, además de que cada cuerpo tendrá sus propios axiomas particulares
(como los axiomas de relación de orden que existen en los reales, pero no en
los complejos) debido a sus características propias. El axioma de clausura nos
dice que al operar dos elementos de un grupo, este también debe pertenecer al
grupo. Esto no se cumple por ejemplo en los irracionales en el caso de 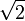 que es irracional,
pero si multiplicamos
que es irracional,
pero si multiplicamos 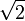 x
x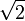 = 2, 2 no pertenece a los irracionales.
= 2, 2 no pertenece a los irracionales.
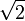 que es irracional,
pero si multiplicamos
que es irracional,
pero si multiplicamos 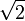 x
x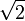 = 2, 2 no pertenece a los irracionales.
= 2, 2 no pertenece a los irracionales.
Los axiomas suelen ser la primera clase o la introducción de
una gran variedad de temas en las matemáticas universitarias, así que
estudiándolas de manera más general nos ahorramos algo de trabajo.



